5-2 과대적합과 과소적합
- 학습 곡선을 통한 과대적합과 과소적합 알아보기
과대적합(overfitting): 모델이 훈련 세트에서는 좋은 성능을 내지만 검증 세트에서는 낮은 성능을 내는 경우
과소적합(underfitting): 훈련 세트와 검증 세트의 성능에는 차이가 크지 않지만 모두 낮은 성능을 내는 경우
훈련 세트의 크기와 과대적합, 과소적합 분석

첫번째 곡선: 과대적합 (분산이 크다: high variance)
두번째 곡선: 과소적합 (편향이 크다: high bias)
세번째 곡선: 과대적합과 과소적합 사이 절충점 찾은 것
에포크와 손실 함수 그래프로 과대적합과 과소적합 분석

왼쪽 그래프: 검증 세트의 손실과 훈련 세트의 손실
(최적점 이후에도 계속해서 훈련세트로 모델을 학습시키면 모델이 과대적합 됨)
(최적점 이전에 학습을 중지하면 과소적합된 모델 생성)
오른쪽 그래프: 세로 축에 손실 대신 정확도
모델 복잡도와 손실 함수의 그래프로 과대적합과 과소적합 분석
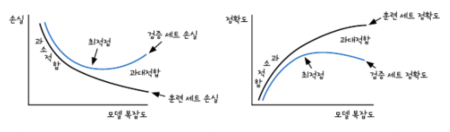
- 적절한 편향 - 분산 트레이드오프 선택
과소적합 된 모델: 편향 되었다
과대적합 된 모델: 분산이 크다.
과소적합된 모델, 과대적합된 모델 사이의 관계: 편향-분산 트레이드오프(bias-variance tradeoff)
1. 검증 손실을 기록하기 위한 변수 추가
def __init__(self, learning_rate=0.1, l1=0, l2=0):
self.w = None
self.b = None
self.losses = []
self.val_losses = []
self.w_history = []
self.lr = learning_rate
2. fit() 메서드에 검증 세트를 전달받을 수 있도록 매개변수 추가
def fit(self, x, y, epochs=100, x_val=None, y_val=None):
self.w = np.ones(x.shape[1]) # 가중치를 초기화합니다.
self.b = 0 # 절편을 초기화합니다.
self.w_history.append(self.w.copy()) # 가중치를 기록합니다.
np.random.seed(42) # 랜덤 시드를 지정합니다.
for i in range(epochs): # epochs만큼 반복합니다.
loss = 0
# 인덱스를 섞습니다
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes: # 모든 샘플에 대해 반복합니다
z = self.forpass(x[i]) # 정방향 계산
a = self.activation(z) # 활성화 함수 적용
err = -(y[i] - a) # 오차 계산
w_grad, b_grad = self.backprop(x[i], err) # 역방향 계산
# 그래디언트에서 페널티 항의 미분 값을 더합니다
w_grad += self.l1 * np.sign(self.w) + self.l2 * self.w
self.w -= self.lr * w_grad # 가중치 업데이트
self.b -= self.lr * b_grad # 절편 업데이트
# 가중치를 기록합니다.
self.w_history.append(self.w.copy())
# 안전한 로그 계산을 위해 클리핑한 후 손실을 누적합니다
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a)+(1-y[i])*np.log(1-a))
# 에포크마다 평균 손실을 저장합니다
self.losses.append(loss/len(y) + self.reg_loss())
# 검증 세트에 대한 손실을 계산합니다
self.update_val_loss(x_val, y_val)
3. 검증 손실 계산
def update_val_loss(self, x_val, y_val):
if x_val is None:
return
val_loss = 0
for i in range(len(x_val)):
z = self.forpass(x_val[i]) # 정방향 계산
a = self.activation(z) # 활성화 함수 적용
a = np.clip(a, 1e-10, 1-1e-10)
val_loss += -(y_val[i]*np.log(a)+(1-y_val[i])*np.log(1-a))
self.val_losses.append(val_loss/len(y_val) + self.reg_loss())
4. 모델 훈련하기
layer3 = SingleLayer()
layer3.fit(x_train_scaled, y_train, x_val=x_val_scaled, y_val=y_val)
5. 손실값으로 그래프 그려 에포크 횟수 지정
plt.ylim(0, 0.3)
plt.plot(layer3.losses)
plt.plot(layer3.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()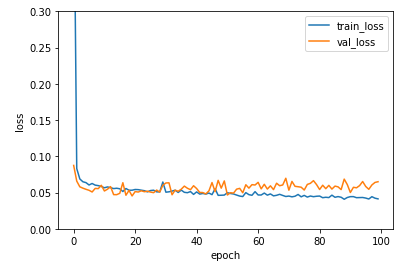
6. 훈련 조기 종료하기
layer4 = SingleLayer()
layer4.fit(x_train_scaled, y_train, epochs=20)
layer4.score(x_val_scaled, y_val)
##출력: 0.9890109890109895-3 규제 방법을 배우고 단일층 신경망에 적용
- 가중치 규제(regularization): 가중치의 값이 커지지 않도록 제한하는 기법
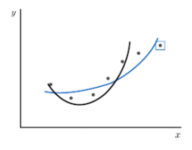
두 그래프 중 완만한 쪽이 성능이 좋음 -> 박스로 표시한 샘플 데이터를 더 잘 표현했기 때문에
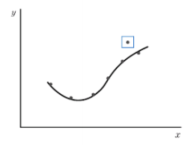
모델이 몇 개의 데이터에 집착하면 새로운 데이터에 적응하지 못하므로 좋은 성능을 가졌다고 할 수 없다
- L1 규제
손실함수에 가중치의 절댓값인 L1 노름(norm)을 추가
L1 노름
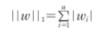
로지스틱 손실 함수에 L1 규제 적용

규제의 양을 조절하는 파라미터 a를 곱한 후 더함

- L1 규제의 미분
L1 규제를 적용한 손실함수의 도함수

가중치 업데이트 식에 적용
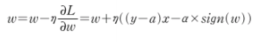
w_grad += alpha * np.sign(w)alpha: 규제 하이퍼파라미터
np.sign(): 배열 요소의 부호를 반환
절편에 대해 규제를 하지 않는다 -> 절편은 모델에 영향을 미치는 방식이 가중치와 다르기 때문에
회귀 모델+L1 규제 = 라쏘 모델(Lasso)
- L2 규제
손실 함수에 가중치에 대한 L2 노름(norm)의 제곱을 더함
L2 노름
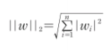
손실 함수 + L2 노름의 제곱 = L2 규제
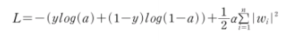
- L2 규제의 미분
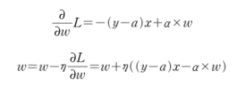
L2 규제는 그레이디언트 계산에 가중치의 값 자체가 포함되므로 가중치의 부호만 사용하는 L1 규제보다 조금 더 효과적
w_grad += alpha * w회귀 모델에 L2 규제를 적용한 것은 릿지 모델(Ridge)
사이킷런에서 릿지 모델을 sklearn.linear_model.Ridge 클래스로 제공
SGDClassifier 클래스에서는 penalty 매개변수를 l2로 지정해서 추가가능
- L1 규제와 L2 규제 정리

※ 해당 내용은 <Do it! 딥러닝 입문>의 내용을 토대로 학습하며 정리한 내용입니다.
'딥러닝 학습' 카테고리의 다른 글
| 6장 2개의 층을 연결 - 다층 신경망 (1) (0) | 2023.03.09 |
|---|---|
| 5장 훈련 노하우 배우기 (3) (0) | 2023.03.08 |
| 5장 훈련 노하우 배우기 (1) (0) | 2023.03.06 |
| 4장 분류하는 뉴런 만들기-이진분류 (3) (0) | 2023.03.05 |
| 4장 분류하는 뉴런 만들기-이진 분류 (2) (0) | 2023.03.04 |



